… y llevan razón quienes me lo dicen y me lo preguntan. “Don Ino, ¿cómo se le ocurre meterse en el berenjenal de geometría y matemáticas si lo suyo es la religión y la historia casi a partes iguales?"
También yo me lo he preguntado muchas veces y, por la complejidad y extensión de una respuesta real y sincera, he dado asentimiento y razón a quienes me lo preguntan. Pero realmente e interiormente, creo (y estoy convencido de ello) que todo está muy relacionado (geometría, matemáticas, religión, historia y arquitectura); demasiado relacionado (¡y eso que no doy el son con la música, que también tiene lo suyo en ese “quadrivium” personal, salvo la arquitectura! Quitando esta última y sustituyéndola por la música, tendríamos así mi “quinquevium” personal).
En las tres adormideras anteriores he intentado demostrar (o, al menos, aproximar y relacionar) ese “quadrivium” propio, batiburrillo entre ciencias y humanidades. No sé si lo estoy consiguiendo o ya lo he conseguido, pero creo que esas cuatro ciencias, a primera vista muy alejadas entre sí, tienen un fuerte nexo en común. Para poder apreciar esa relación tratemos de contestar a la siguiente pregunta: ¿qué edificio de los que ahora se construyen será capaz de resistir en pie sin afecciones graves tantos siglos como tantas iglesias y catedrales han superado? Ese largo paso del tiempo es la mejor respuesta a la pregunta y el mejor aval sobre la eficacia de la aplicación y relación de esas “cuatro ciencias” y de los conocimientos que los constructores de aquellas épocas antiguas poseían. Pero, al contrario de lo que sucede en la actualidad, esos conocimientos no se divulgaban con la misma facilidad y rapidez con la que se divulgan hoy día.
Todos los grandes descubrimientos en invenciones, agricultura, metalurgia, técnicas diversas, artes, etc., implicaban en sus comienzos el secreto: se suponía que sólo los “iniciados” en los secretos del oficio estaban en condiciones de garantizar los buenos resultados de cualquiera de aquellas operaciones. Los gremios vigilaban escrupulosamente el acceso a los nuevos miembros y controlaban la enseñanza de estas disciplinas que debían ser asimiladas poco a poco, superando con trabajo y paciencia los distintos grados establecidos. Ya en los Estatutos de Ratisbona se advertía de “(…) enseñar a nadie (…) cómo extraer el alzado de la planta”. Por ello, y sorprendentemente para nuestra mentalidad actual, los “architectus” o personas capaces de concebir y construir edificios tan duraderos y bellos, padecieron un protagonismo social de escasa relevancia. Aun así, consiguieron que la arquitectura religiosa y, por ende, la geometría sagrada que en ella se aplicaba, fuera una manifestación voluntaria de la espiritualidad de su tiempo. Se trataba de construir la casa de Dios, de acoger a los fieles mostrando su presencia del modo más bello posible, transmitiendo la palabra y el ejemplo de un Cristo justiciero, premiando a los justos y castigando a los pecadores a las más terribles penas del infierno. Así, Dios es también arquitectura, inequívoca expresión del espíritu cristiano que lo impregna todo. De esta forma, el Arte se transforma así en historia, dando respuesta a la historia. Por lo tanto, no nos debe extrañar la dualidad entre arte y matemáticas, ya que los hombres cultos de otras épocas no establecían diferencia alguna entre el área de ciencias y el área de humanidades.
Quizás la mejor manera de demostrar la afirmación anterior la podemos encontrar en el número de oro, a partir del cual se forma o se crea el rectángulo áureo, creando, a su vez, la proporción áurea, divina proporción, media áurea, sección áurea o, incluso, proporción biológica (luego veremos porqué este último nombre), todos ellos nombres o maneras de expresar todo aquello que parte o se inicia con el número de oro como medida fundamental y básica.
El número de oro fue uno de los secretos privativos del gremio de constructores al que hacíamos alusión anteriormente, el cual se iba transmitiendo “secretamente” entre ellos. Durante la Edad Media, el número de oro y la sección áurea eran considerados como algo de origen divino, la encarnación de la perfección creadora de Dios y, por lo tanto, fueron consignados en sus templos. Los claustros de muchos monasterios románicos seguían esta proporción, así como la arquitectura gótica, que la empleó de manera constante en la construcción de sus primeras catedrales.
Claustro del monasterio de Silos. Burgos.
Ya desde muy antiguo, la proporción áurea fue apreciada como una relación mística entre los números y su manifestación en el ser humano. Considerada como divina en sus composiciones e incalculable en sus significados, la “sectio aurea” (nombre latino de la sección áurea) ya aparece en el “Timeo” de Platón y en el “Libro VI de los Elementos” de Euclides. Leonardo da Vinci le dio el nombre de “número áureo” a este número irracional y Lucca Pacioli lo “bautizó” como “Divina Proporción”, quién escribió un libro exaltando sus propiedades tanto geométricas como aritméticas. Sin embargo, fue Kepler el primero que observó la sección áurea en la naturaleza, en las plantas en particular (más adelante retomaremos esta última parte con algo más de profundidad).
Bueno, vamos a dejarnos de meter morralla en la adormidera y vayamos al meollo de la cuestión, que no es otro que el número de oro y la sección áurea y cómo está presente en más facetas de nuestra vida de lo que nosotros realmente creemos.
Una primera definición básica que nos va a permitir acercarnos a conocer el número de oro o la sección áurea podría ser ésta: “La sección áurea es la división armónica de un segmento en media y extrema razón. Es decir, que el segmento menor es al segmento mayor, como éste es a la totalidad. De esta manera se establece una relación de tamaños con la misma proporcionalidad entre el todo dividido en mayor y menor. Esta proporción o forma de seleccionar proporcionalmente una línea se llama proporción áurea”.
Esto, dicho así, “de carrerilla”, nos puede resultar un poco o totalmente “cursi” y pedante, por lo que vamos a realizar una demostración práctica de la definición académica anterior para poder entenderla mejor y de manera definitiva.
Tomemos un segmento de longitud uno
(1) y hagamos en él la división expuesta anteriormente:
Aplicando la proporción áurea obtenemos la siguiente ecuación que tendremos que resolver:
Una de las soluciones de esta ecuación (la solución positiva de las dos posibles soluciones de una ecuación de segundo grado) es:
cuyo resultado es el número de oro:
1’61803398874989484824 ……
Por lo tanto, la relación entre las dos partes en las que dividimos el segmento es el número de oro. Por la misma razón, el rectángulo cuyos lados están en una proporción igual a la razón o proporción áurea es llamado “rectángulo áureo”.
En la antigüedad y más concretamente los griegos, ya hablaban de este número de oro y de este rectángulo áureo. El signo habitual que ellos tenían para representarlo en los textos de matemáticas no era la letra griega que conocemos en la actualidad, Φ, sino que utilizaban el signo “τ”, del griego τομη, que significa “corte” o “sección”. La actual denominación Φ, (phi en mayúscula o minúscula) la formalizó el matemático Mark Barren en honor a Fidias, ya que ésta es la primera letra de su nombre en griego: Φειδιας.
¿No os pica la curiosidad preguntarse por qué los griegos se preocuparon por dividir un segmento en extrema y media razón (la división comentada anteriormente)? ¿No tenían otra cosa que hacer que preocuparse por “partir algo en dos trozos”? No, no es eso. Tratemos, una vez más, de analizar la historia con los ojos de aquella época y no con los nuestros de esta época.
Los griegos siempre se caracterizaron por exaltar la belleza; no hay más que ver las estatuas y bustos que tallaban. Por lo tanto, la contestación a las preguntas anteriores es muy sencilla y tiene que ver con la armonía y con la belleza, esa belleza que siempre resaltaron y dignificaron. La percepción de la belleza para ellos radicaba en la proporción áurea. Cuando matemáticamente algo se aproximaba a Φ o al número de oro, se percibía como más bello, más perfecto; lo pequeño es a lo grande como lo grande es al todo. Esto último lo llevaron inevitablemente a una serie de medidas con las que creaban el concepto de proporción.
La proporción, entonces, viene dada por la relación entre las dimensiones de dos o más partes de un todo, o entre las partes respecto a la totalidad. También se identifica con las relaciones de tamaño que guardan unas formas con las formas de su entorno. El tamaño es una relación relativa, ya que las cosas por sí mismas no son ni grandes ni pequeñas, hasta que no son comparadas con otras de su alrededor. Las proporciones de las formas artísticas a lo largo de la historia se han basado en conceptos geométricos y matemáticos, así como en su función. Y buscando siempre el ideal de la belleza y, por tanto, de proporción, se llegó hasta la “divina proporción” encontrada mediante la “proporción áurea”, cuya razón era definida por el número de oro, que a su vez, desde la divina proporción, se llegó hasta la creación del “rectángulo de oro” o “rectángulo áureo” que no es sino un tratamiento compositivo para conseguir la armonía y la estética mediante una estructura bella y equilibrada.
Un ejemplo para tratar de explicar y afirmar esto último lo tenemos en un experimento que se puede llevar a cabo de una manera fácil y sencilla. Veamos.
Si pidiésemos a un grupo de personas
que eligieran un rectángulo entre unos cuántos de diferentes proporciones entre
su anchura y su altura, comprobaríamos que el rectángulo mayoritariamente
elegido es aquel cuyos lados cumplen esa relación áurea. Lo mismo ocurriría si
les pidiésemos que ellos mismos lo dibujaran.
Tomando como ejemplos los cuatro rectángulos representados en la imagen anterior, del grupo de personas elegido en el experimento anterior, mayoritariamente elegirían el rectángulo azul, el que se encuentra representado en la parte inferior derecha (una primera curiosidad de este rectángulo con estas dimensiones es que tiene las mismas proporciones y el mismo formato que el DNI o las tarjetas de crédito). El rectángulo rojo de la parte superior izquierda tiene un formato de 16/9, el de las televisiones panorámicas; el amarillo, en la parte superior derecha, tiene un formato de 36/24, formato de las fotografías y diapositivas; el rectángulo verde, inferior izquierda, es el habitual de las hojas y folios, A0, A1, A2, A3, A4. . . , es decir, el formato de raíz de 2, ya que si las longitudes de los lados del rectángulo fueran A y B, podríamos comprobar que A dividido entre B daría como resultado la raíz de dos, resultado que se seguiría manteniendo si fuéramos doblando este mismo rectángulo por la mitad del lado más largo; siempre tendría un valor de raíz de dos.
Ahora que ya sabemos lo que es y cuánto vale el número de oro, la proporción áurea y las formas y proporciones de un rectángulo áureo, vamos a aprender una forma fácil y sencilla (¡para toda la familia!) de dibujar un rectángulo áureo.
Dibujamos un cuadrado de lado 1 (uno) y marcamos el punto medio de uno de sus lados, el horizontal, por ejemplo. Lo unimos con uno de los vértices del lado opuesto y, con un compás, llevamos esa distancia sobre el lado inicial; de esta manera obtenemos el lado mayor del rectángulo.
La
distancia
Si el lado del cuadrado vale 2
unidades es claro que el lado mayor del rectángulo vale:
por
lo que la proporción entre los dos lados es:
nuestro
número de oro.
¿Recordáis la forma que tenía aquél rectángulo azul del experimento explicado anteriormente aplicado a un grupo de personas? ¿Os acordáis que dijimos que ese rectángulo azul que elegirían la mayoría de los participantes tenía el mismo formato que nuestro DNI actual y el mismo formato que nuestras tarjetas de crédito, tarjetas de transporte, carnet de conducir, tarjeta sanitaria, etc? Mirad la siguiente ilustración de un DNI:
DNI en formato rectángulo áureo
¿Sorprendidos? No creo; más bien aliviados con esta imagen que demuestra claramente cómo convivimos diariamente con los rectángulos áureos y las proporciones áureas. ¡Todos los conocimientos que consiguieron en la antigüedad, aún perduran y perdurarán en nuestra vida, como no podía ser de otra manera. Ya lo dice el refrán: “Donde no haya un viejo, hay que buscarlo”. Para viejo, yo mismo, … o ellos mismos, más viejos que yo.
Bien. Después de estos aprendizajes “proporcionales y divinos” y demostración actualizada del rectángulo áureo, continuemos con más creaciones rectangulares, proporcionales y divinas.
Utilicemos ahora el procedimiento euclidiano para dividir un
segmento AB en “extrema y media razón”: “Dado el segmento “AB”, trazamos la
perpendicular “BD” de la misma longitud que “AB”; obtenemos el punto medio “C”
de “BD”. Trazamos el segmento “AC” y, con centro en “C”, trazamos una
circunferencia por “B”, siendo “E” el punto donde corta el segmento “AC”. Con
centro en el punto “A”, trazamos la circunferencia por “E”. El punto “M”, donde
esta circunferencia corta el segmento “AB”, es la sección áurea de “AB”.
Procedimiento de Euclide
Los rectángulos áureos, además de mantener la proporción áurea en la relación entre su anchura y su altura, tienen otra curiosa propiedad: al quitarles el cuadrado formado por el lado más pequeño (lo que sería la altura del rectángulo áureo) queda un rectángulo con las mismas proporciones que el original (otro rectángulo áureo). Mediante este mismo procedimiento de replicación, ascendente o descendente, creciente o decreciente, podríamos obtener una espiral a partir de una sucesión de arcos de circunferencia inscritos en los sucesivos rectángulos áureos, tales que las correspondientes cuerdas consecutivas estarían en proporción áurea y formando un ángulo de 90º. La espiral que se construye con ellos se denomina “espiral áurea”.
Cualquier
espectador queda fascinado por la belleza de estas espirales, en las cuales posiblemente
emana su poder para crearse, siguiendo una misma regla en cada caso, desde lo
infinitesimal hasta lo infinito.
¿No creéis que no estaría de más saber construir también una espiral áurea al igual que hemos aprendido a dividir una recta en la proporción áurea primero y construir un rectángulo áureo después? ¡Vamos allá!
Primeramente partimos de un rectángulo áureo “ABCD” y lo dividimos
de tal forma que creamos dentro del mismo un cuadrado con una longitud de lado
igual al lado más pequeño del rectángulo áureo del que hemos partido (“AD” en
este caso). Ahora tenemos un cuadrado “AEFD” y otro rectángulo áureo “EBCF”,
más pequeño que el inicial, pero rectángulo áureo al fin y al cabo. Continuamos
realizando el mismo proceso anterior hasta conseguir el punto “O”, que no es
otro que el punto donde se cortan las diagonales, “AC” y “BF”, correspondientes
a los rectángulos áureos “ABCD” y “EBCF”, las cuales se cruzan perpendicularmente.
Este punto “O es llamado “polo de la
espiral equiangular” que pasa por los cortes áureos “D, E, G, J, F” etc.
Si nos fijamos en las siguientes figuras geométricas podemos apreciar mucho mejor el proceso de creación de la espiral áurea. Una vez que hemos construido la sucesión de rectángulos áureos acoplados de la forma descrita anteriormente, al unir mediante un arco dos vértices opuestos de cada uno de los cuadrados obtenidos, utilizando como centro de la misma otro de los vértices del mismo cuadrado, se genera la curva espiral también llamada la “Espiral de Durero”. Hay que decir y que recordar que el crecimiento de nuestra espiral se da en proporción geométrica.
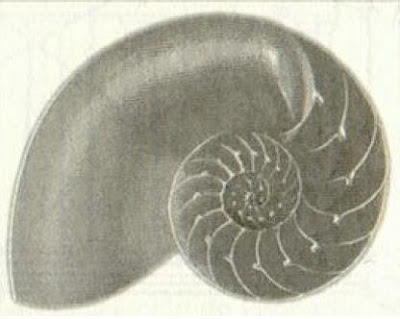
Esta forma constante de espiral aparece, una y otra vez, en las caracolas,
en los remolinos en el agua, remolinos oceánicos, los brazos de los ciclones,
en las galaxias, etc. Veamos unas imágenes de algunas de ellas.
Caracola
Remolino de agua o remolino oceánico
Galaxia
del Remolino (M51)
Ciclón Andrés, frente a las costa de México en el 2015
Imágenes y demostraciones de la espiral áurea hemos podido apreciar anteriormente, pero no hemos ilustrado ni demostrado ninguna edificación arquitectónica ni obra artística que contenga o esté basada o relacionada con el número de oro o con el rectángulo áureo. Al inicio dijimos que los griegos ya se “entretenían” buscando la “proporción divina”, pero en esa época de la Antigüedad nos hemos quedado; no hemos avanzado más hasta la Espiral de Durero y el formato del DNI actual. Podríamos decir que hemos tocado los dos extremos, pero no lo hemos hecho dentro de ambos extremos. Veamos a partir de ahora algunas edificaciones y obras artísticas que tienen relación con el número de oro, rectángulo áureo y la proporción divina.
Podríamos comenzar por el Partenón de Atenas.
Su realización fue encargada por Pericles a los
arquitectos Calícrates e Ictinios, bajo la supervisión de Fidias entre los años 447 y 432 a.C. En su
estructura arquitectónica, tanto los rectángulos que forman la fachada como los
de la planta son rectángulos áureos, estando totalmente basado en la sección
dorada, tanto su anchura como su altura y su profundidad. La distribución de
sus columnas y detalles se encuentran en esta misma proporción. El número áureo aflora para
establecer las dimensiones de toda la edificación y disponer los detalles
escultóricos. Φ surge expresamente en las razones: AB/CD, AC/AD, CD/CA, DE/EA,
según análisis geométricos.
El Partenón
Si se miden las dimensiones del exterior del Partenón, se descubre que no solo forma un rectángulo áureo, sino que también hay muchos otros rectángulos áureos entre las columnas. El uso de la proporción áurea explica la genialidad y la belleza de este ejemplo de arquitectura sagrada.
El Partenón
Otra edificación antigua relacionada con el proporción áurea sería el Templo de Ceres, en Paestum (460 a.C.). Al igual que en la mayoría de los templos dóricos, se advierte que la construcción de la fachada está erigida según un sistema de triángulos áureos, por lo que ya tendríamos inmiscuido nuestro número de oro.
Templo de Ceres
Vayámonos ahora a Florencia, capital del Renacimiento italiano. En esta ciudad nos fijamos en la iglesia de Santa María Novella, obra de León Battista Alberti (1404-1472), artista matemático, autor de tratados en los que las matemáticas se ponen al servicio de la pintura y del arte en general. Miramos la fachada de esta iglesia florentina.
Los elementos y composición de esta fachada se relacionan unos con otros en la proporción áurea de los griegos, Φ = (1 + √5)/2, aunque usa también otras proporciones basadas en el cuadrado y asociadas, por tanto, al número √2. Pero su belleza, sin duda, deriva de la proporción matemática y geométrica de sus elementos.
Santa María Novella. Florencia
Analicemos su portada.
Primeramente enmarcamos la portada de la basílica en un cuadrado. Construimos tres rectángulos áureos a partir de las proporciones entre los lados. El triángulo isósceles del tímpano se divide en dos triángulos rectángulos cuyos catetos están en proporción áurea. Se construye, de esta forma, una primera espiral a partir de ellos. El rectángulo formado por la puerta y el arco de medio punto que hay sobre él también mantiene la proporción áurea. Ya, por último, el rectángulo central que abarca el piso superior y la parte correspondiente de la inferior también tiene esta proporción.
Todos los elementos descritos
anteriormente podrían representarse de la siguiente forma en la fachada:
Rectángulos áureos, espirales áureas; número de oro en toda su extensión.
Dos
edificaciones más con las mismas proporciones áureas:
Arco de Septimio Severo
Puerta de Bagdad
Las proporciones armoniosas para el
cuerpo que estudiaron los griegos y romanos las plasmó en este dibujo Leonardo da Vinci. Sirvió para
ilustrar el libro “La Divina Proporción” de Luca Pacioli editado en 1509.
En este dibujo se establece un canon de belleza humana basado precisamente en la divina proporción. Así, esta proporción, generadora de la armonía y belleza, capturaría el reflejo de Dios en la criatura humana, a quien “creó a su imagen y semejanza”. El número de oro está presente en las numerosas proporciones que se pueden establecer en el dibujo. La circunferencia que aparece tiene como centro el ombligo y como radio la distancia de éste a los pies. El rectángulo formado por la altura completa del hombre y la mitad del lado del cuadrado (oculto) circunscrito a la circunferencia dibujada es áureo. Es decir, la divina proporción es la razón entre la altura del hombre y la distancia del ombligo a los pies. Es curioso que en el niño recién nacido, el ombligo divide normalmente al cuerpo en dos partes iguales, papel que pasa a ocupar el aparato genital en el hombre adulto armonioso.
Ahora
una pintura, esta vez de Salvador Dalí: Leda Atómica.
“Leda atómica”. Dalí
Esta pintura, observada o mirada de manera “natural”, no parece incitarnos a buscar nada “raro” en ella atendiendo al tema tratado del número de oro o proporción áurea. Pero si atendemos a unos bocetos primigenios del autor utilizados para realizar dicha pintura, se puede observar fácilmente que en él aparece inscrito un círculo y, dentro de él, aparece también un pentágono estrellado regular. Este pentágono era el distintivo de los pitagóricos.
El pentágono regular siempre ha poseído unas connotaciones esotéricas. Para las invocaciones a los espíritus, al diablo, etc., se valen de una escenografía donde aparece habitualmente el pentágono regular como elemento intermedio, como puerta de acceso entre la realidad y la irracionalidad.
La siguiente figura ilustra lo que
acabo de comentar.
Boceto de “Leda atómica”. Dalí
A poco que repasemos la vida y obra de Salvador Dalí, podríamos hacernos una idea de cómo tenía que preparar cada obra que comenzaba, cada boceto que realizaba, etc. Pero, aun así, ¿realmente Dalí realizó y terminó esta obra a partir del boceto mostrado anteriormente, un pentágono regular inscrito dentro de un círculo? ¿Tuvo en cuenta esta geometría sagrada del número de oro o proporción áurea? No sé. Quizás fuera mejor realizarnos preguntas de este tipo al final de esta larguísima adormidera, a modo de epílogo.
Como final de esta parte de la geometría sagrada dedicada al número de oro, proporción áurea, etc., muestro algunas imágenes que relacionan la naturaleza con dicha proporción áurea.
Al comienzo, recordaréis que fue Kepler el primero que relacionó todo este número y proporción con la naturaleza. Así es. En la naturaleza también aparece la proporción áurea en el crecimiento de las plantas, distribución de las escamas de las piñas, la distribución de las hojas en un tallo, dimensiones de un insecto y pájaros y la formación de caracolas o desarrollo de la espiral de los caracoles (ya vistas anteriormente con bastante detenimiento), desarrollo de los cuernos de las cabras, etc. Cualquier espectador queda fascinado por la belleza de todas estas formas y espirales que posiblemente emana de su poder para crearse, siguiendo una misma regla en cada caso, desde lo infinitesimal hasta lo infinito.
Semillas de
girasol
Conos de un pino
Tal y cómo he comentado antes, no estaría de más que, como final de todo este largo capítulo dedicado a la geometría sagrada y al número y proporción áurea y a modo de epílogo, nos hiciéramos algunas preguntas acerca de todo lo visto hasta ahora en estos capítulos o adormideras.
Más que geometría sagrada, ¿no puede ser una geometría buscada y encontrada por el hombre fruto de su trabajo y aprendizaje empírico? ¿No puede ser un reflejo de los buscado y encontrado a partir de la experiencia y la observación detenida y progresiva de la naturaleza? ¿No concuerda eso mucho más que cualquier otra elucubración fruto de una búsqueda intencionada y, por consiguiente, encontrada a la fuerza y encajada “a palos” en lo que interesa en ese momento? ¿No puedo comenzar esa geometría a partir de personas como Pitágoras o Platón que dedicaron su vida a la búsqueda de respuestas a todo un mundo desconocido que los rodeaba? ¿Y si todo esto fuera una invención más del hombre para responder a preguntas muchas veces sin respuesta amparándose en elucubraciones fantasiosas y misteriosas más cercanas a la autocomplacencia que a la realidad misma?
Preguntas y más preguntas. ¿Respuestas? El tiempo lo dirá.
También el tiempo me ha dicho que tengo que parar un poco en analizar y tratar de explicaros cualquier tema que tenga que ver con el mundo del Arte Románico, por pequeña que sea, o por pequeña relación tenga con dicho arte, como es el caso de la Geometría Sagrada.
¡Hasta pronto!